• 前向传播（forward pass）指的是：按顺序（从输入层到输出层）计算和存储神经网络中每层的结果。

• 反向传播（backward propagation或backpropagation）指的是计算神经网络参数梯度的方法。简 言之，该方法根据微积分中的链式规则，按相反的顺序从输出层到输入层遍历网络。该算法存储了 计算某些参数梯度时所需的任何中间变量（偏导数）。

• 计算图：具体直接看实例，图1，图2，图3

问题：前向传播具体是计算什么？存储什么？反向传播怎么计算梯度？

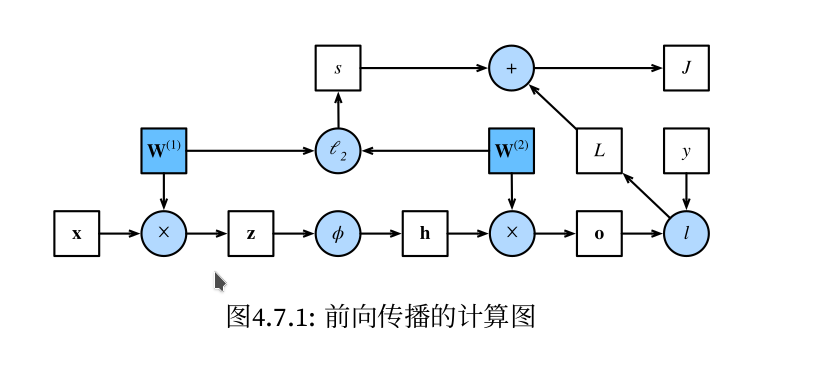
图1（即图4.7.1）来自《动手学深度学习》一书。本节主要内容均来自此书对应章节。 简单网络（单隐藏层网络）相对应的计算图，其中正方形表示变量，圆圈表示操作符。左下角表示输 入，右上角表示输出。注意显示数据流的箭头方向主要是向右和向上的。

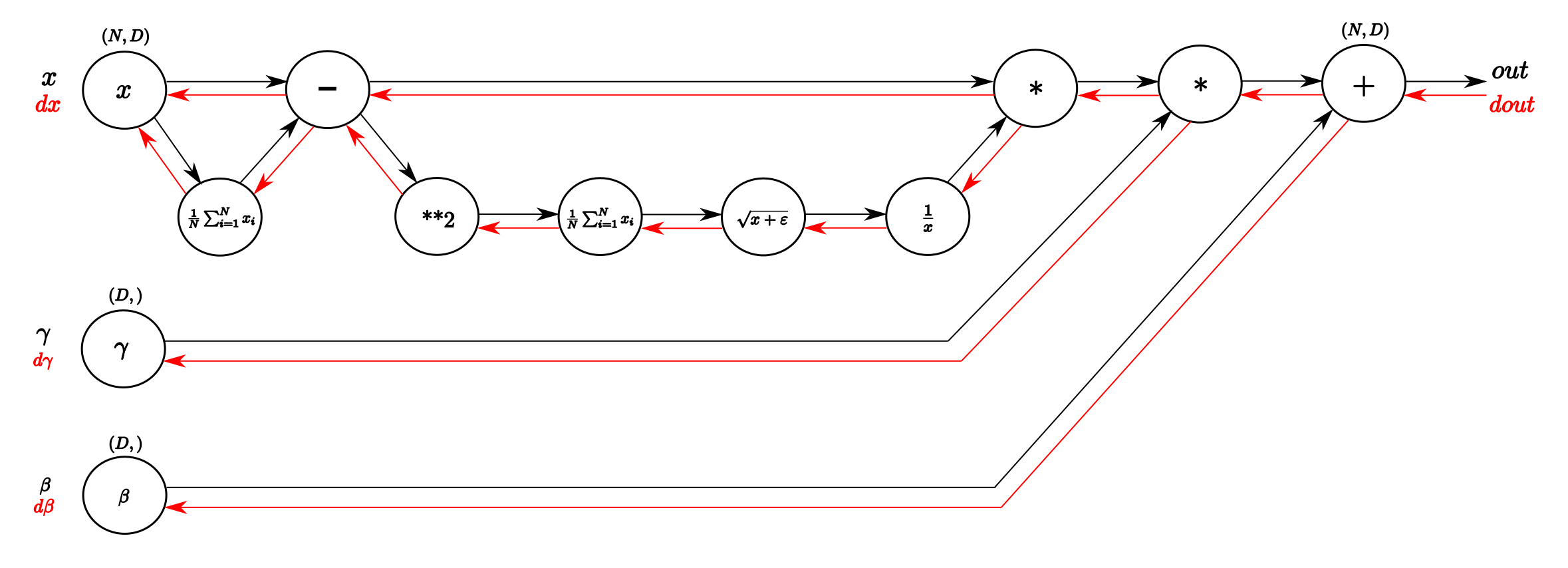图2 Computational graph of the BatchNorm-Layer. From left to right, following the black arrows flows the forward pass. The inputs are a matrix X and gamma and beta as vectors. From right to left, following the red arrows flows the backward pass which distributes the gradient from above layer to gamma and beta and all the way back to the input. (来自此博客)

在并行运算中，使用原地分区不一定总是比使用额外空间更好。

• 内存充足、数据量大：使用额外空间分区，便于并行化且编程简洁。
• 内存有限、数据量中等：使用原地分区，减少内存开销。

Bernstein 基函数是贝塞尔曲线（Bezier curve）的一个重要组成部分。它们定义了一组基函数，通 常用于表示参数化曲线，尤其是 Bézier 曲线。对于 Bézier 曲线，Bernstein 基函数定义如下：

对于给定的阶数 $n$，第 $i$ 个 Bernstein 基函数 $B_{i,n}(t)$ 的表达式为：

$$ B_{i,n}(t) = \binom{n}{i} t^i (1 - t)^{n-i} $$

其中：

• $n$ 是 Bézier 曲线的阶数（即控制点的数量减 1）。
• $i$ 是当前的基函数索引，取值范围为 $0 \leq i \leq n$。
• $t$ 是参数，取值范围通常为 $0 \leq t \leq 1$。
• $\binom{n}{i}$ 是二项式系数，表示为 $\frac{n!}{i!(n-i)!}$。

## Bernstein 基函数的特性：

1. 非负性：在 $0 \leq t \leq 1$ 的范围内，所有 Bernstein 基函数的值都是非负的。
2. 分片多项式性：Bernstein 基函数是 $t$ 的多项式函数。
3. 端点插值：当 $t = 0$ 或 $t = 1$ 时，只有一个基函数的值不为 0，而该函数的值为 1。 这意味着 Bézier 曲线会精确地通过其起点和终点。
4. 分区一致性：所有基函数在任意 $t$ 下的和为 1，即 $$ \sum_{i=0}^{n} B_{i,n}(t) = 1 $$ 这一特性确保了 Bézier 曲线的凸包性质，即曲线位于控制点构成的凸包内。

Bernstein 基函数在图形学、曲线和曲面的建模中应用广泛，特别是在 Bézier 曲线和 Bézier 曲面 的表示中起到了基础作用。