spectral_decomposition
Table of Contents
NOTE: For more content see ThinkDSP
DFT is a mathematical idea, and FFT is an algorithm for computing DFT.
Spectral decomposition: The idea that any signal can be expressed as the sum of sinusoids with different frequencies.
#
What is a signal?
A signal represents a quantity that varies in time. (pretty abstract,eh?) A concrete example: sound. A sound signal represents variations in air pressure over time.
Periodic signals: The signals that repeat themselves after some period ot time.
A sinusoid which means it has the same shape as the trigonmetric sine function. And a sinusoid contains only one frequency component, so its spectrum has only one peak.
cycles: the full repetitions in a periodic signal. period: the duration of each cycle. frequency: the number of cycles per second, which is the inverse of period. - the units of frequency are cycles per second, or Hertz (Hz). - strictly speaking, the number of cycles is a dimensionless number, so a Hertz is really a “per second”.
A microphone is a device that measures these variations and generates an electrical signal that represents sound. A speaker is a device that takes an electrical signal and produce sound. They are called transducers because they transduce, or convert, signals from one form to another.
#
Discrete Fourier transform (DFT)
DFT is a mathematical idea which takes a signal and produces its spectrum. The spectrum is the set of sinusoids that add up to produce the signal.
And the FFT (Fast Fourier transform) is an algorithm which is an efficient way to compute the DFT.
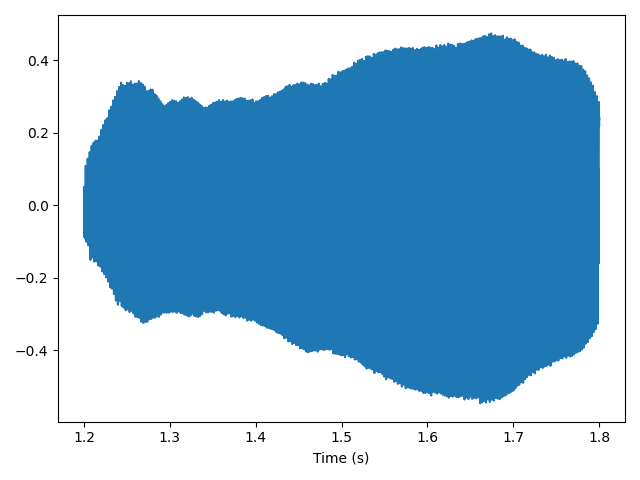
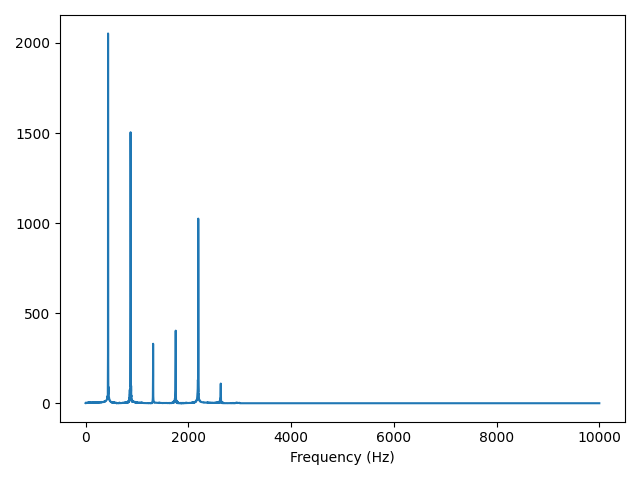
The lowest frequency component is called the fundamental frequency. If the fundamental frequency has the largest amplitude, it is also the dominant frequency. Normally the perceived pitch of a sound is determinded by the fundamental frequency, even if it is not dominant.
The fundamental frequency of this signal is near 440 Hz, the other spikes in the spectrum are at frequencies 880, 1320, 1760, and 2200, which are integer multiples of the fundamental. These components are called harmonics because they are musically harmonious with the fundamental:
- 440 is the frequency of A4, the fundamental frequency.
- 880 is the frequency of A5, one octave higher than the fundamental. An octave is a doubling in frequency.
- 1320 is approximately E6, which is a perfect fifth above A5.
- 1760 is A6, two octave above the fundamental.
- 2200 is approximately C#7, which is a major third above A6.
NOTE: Given the harmonics and their amplitudes, you can reconstruct the signal by adding up sinusoids.
Some code about signal/wave :
# More codes here are ignored ...
class Signal:
"""Represents a time-varying signal."""
def __add__(self, other):
"""Adds two signals.
other: Signal
returns: Signal
"""
if other == 0:
return self
return SumSignal(self, other)
__radd__ = __add__
@property
def period(self):
"""Period of the signal in seconds (property).
Since this is used primarily for purposes of plotting,
the default behavior is to return a value, 0.1 seconds,
that is reasonable for many signals.
returns: float seconds
"""
return 0.1
def plot(self, framerate=11025):
"""Plots the signal.
The default behavior is to plot three periods.
framerate: samples per second
"""
duration = self.period * 3
wave = self.make_wave(duration, start=0, framerate=framerate)
wave.plot()
def make_wave(self, duration=1, start=0, framerate=11025):
"""Makes a Wave object.
duration: float seconds
start: float seconds
framerate: int frames per second
returns: Wave
"""
n = round(duration * framerate)
ts = start + np.arange(n) / framerate
ys = self.evaluate(ts)
return Wave(ys, ts, framerate=framerate)
class Sinusoid(Signal)
# More codes here are ignored ...
def evaluate(self, ts):
# (self.freq * ts) is the number of cycles since start time
# Multiplying 2*np.pi converts from cycles to phases
# and phases can be view as "cycles since start time expressed in radians"
# the func is cos or sin, returns value between -1 and 1
phases = 2*np.pi * (self.freq * ts) + self.offset
ys = self.amp * self.func(phases)
return ys
class Wave:
"""Represents a discrete-time waveform."""
def __init__(self, ys, ts=None, framerate=None):
"""Initializes the wave.
ys: wave array
ts: array of times
framerate: samples per second
"""
self.ys = np.asanyarray(ys)
self.framerate = framerate if framerate is not None else 11025
if ts is None:
self.ts = np.arange(len(ys)) / self.framerate
else:
self.ts = np.asanyarray(ts)
def copy(self):
"""Makes a copy.
Returns: new Wave
"""
return copy.deepcopy(self)
def __len__(self):
return len(self.ys)
@property
def start(self):
return self.ts[0]
@property
def end(self):
return self.ts[-1]
@property
def duration(self):
"""Duration (property).
returns: float duration in seconds
"""
return len(self.ys) / self.framerate
def __add__(self, other):
"""Adds two waves elementwise.
other: Wave
returns: new Wave
"""
if other == 0:
return self
assert self.framerate == other.framerate
# make an array of times that covers both waves
start = min(self.start, other.start)
end = max(self.end, other.end)
n = int(round((end - start) * self.framerate)) + 1
ys = np.zeros(n)
ts = start + np.arange(n) / self.framerate
def add_ys(wave):
i = find_index(wave.start, ts)
# make sure the arrays line up reasonably well
diff = ts[i] - wave.start
dt = 1 / wave.framerate
if (diff / dt) > 0.1:
warnings.warn(
"Can't add these waveforms; their " "time arrays don't line up."
)
j = i + len(wave)
ys[i:j] += wave.ys
add_ys(self)
add_ys(other)
return Wave(ys, ts, self.framerate)
__radd__ = __add__
# Write a function called stretch that takes a Wave and a stretch factor and speeds up
# or slows down the wave by modifying ts and framerate.
def stretch(wave, factor):
"""
if 0 < factor < 1, speed up, else slow down
"""
wave.ts *= factor
wave.framerate /= factor