• 前向传播（forward pass）指的是：按顺序（从输入层到输出层）计算和存储神经网络中每层的结果。

• 反向传播（backward propagation或backpropagation）指的是计算神经网络参数梯度的方法。简 言之，该方法根据微积分中的链式规则，按相反的顺序从输出层到输入层遍历网络。该算法存储了 计算某些参数梯度时所需的任何中间变量（偏导数）。

• 计算图：具体直接看实例，图1，图2，图3

问题：前向传播具体是计算什么？存储什么？反向传播怎么计算梯度？

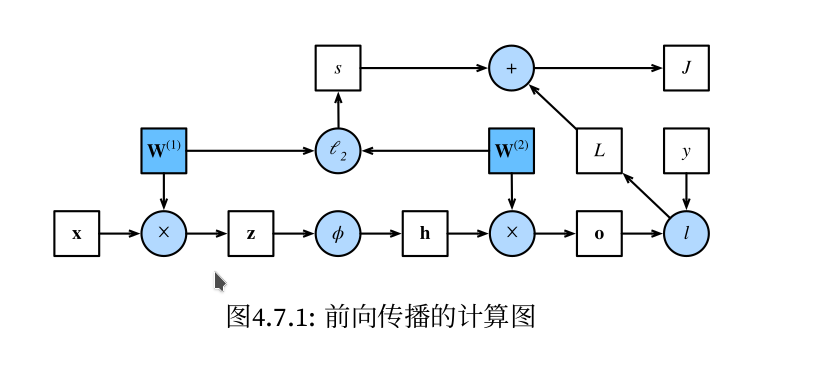
图1（即图4.7.1）来自《动手学深度学习》一书。本节主要内容均来自此书对应章节。 简单网络（单隐藏层网络）相对应的计算图，其中正方形表示变量，圆圈表示操作符。左下角表示输 入，右上角表示输出。注意显示数据流的箭头方向主要是向右和向上的。

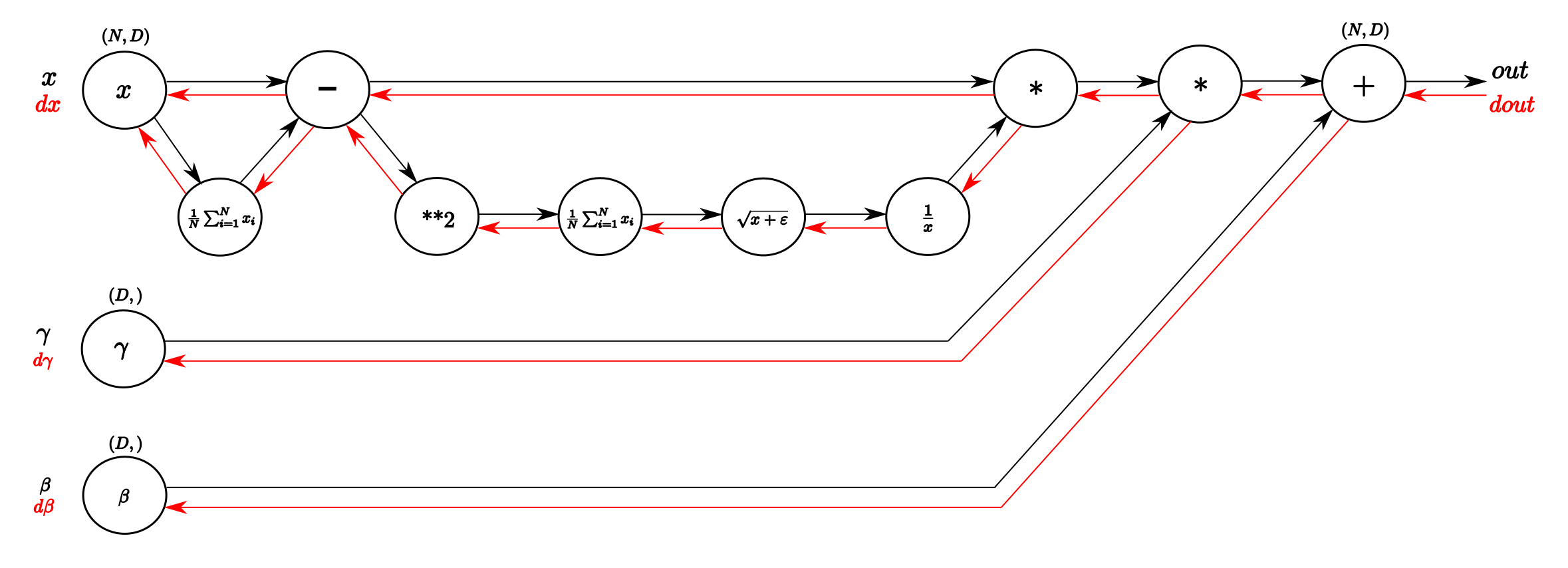图2 Computational graph of the BatchNorm-Layer. From left to right, following the black arrows flows the forward pass. The inputs are a matrix X and gamma and beta as vectors. From right to left, following the red arrows flows the backward pass which distributes the gradient from above layer to gamma and beta and all the way back to the input. (来自此博客)

# 前向传播具体计算的内容包括：

中间变量$z$: $$ z = W^{(1)} x $$

输入样本是 $x \in \mathbb{R}^d$，隐藏层的权重参数 $W^{(1)} \in \mathbb{R}^{h \times d}$

将中间变量$z \in \mathbb{R}^h$通过激活函数$\phi$后，可得到隐藏层激活向量： $$ h = \phi(z) $$

假设输出层参数只有权重$W^{(2)} \in \mathbb{R}^{q \times h}$，以下式子可计算输出层变量， 这是一个长度为$q$的向量： $$ o = W^{(2)} h $$

记损失函数为$\text{loss_fn()}$，样本标签为$y$（通常是独热编码向量），可以计算单个数据样本的误差： $$ L = \text{loss_fn}(o, y) $$

根据$L_2$正则化的定义¹，给定超参数$\lambda$，正则化项为 $$ s = \frac{\lambda}{2} (||W^{(1)}||^{2}_{F} + {||W^{(2)}||}^{2}_{F}) $$

其中矩阵的Frobenius范数²是将矩阵展平（flatten）为向量后应用$L_2$范数的结果。最后，模 型在给定数据样本上的正则化损失为： $$ J = L + s $$

通常将$J$称为目标函数（objective function）。也就是用于最优化（optimization）求解的函数。

以上只是前向传播故事的一部分（出于方便入门理解的初衷？），实际上，前向传播过程还会计算和 存储本地梯度值（local gradient）…

# 故事的另一部分

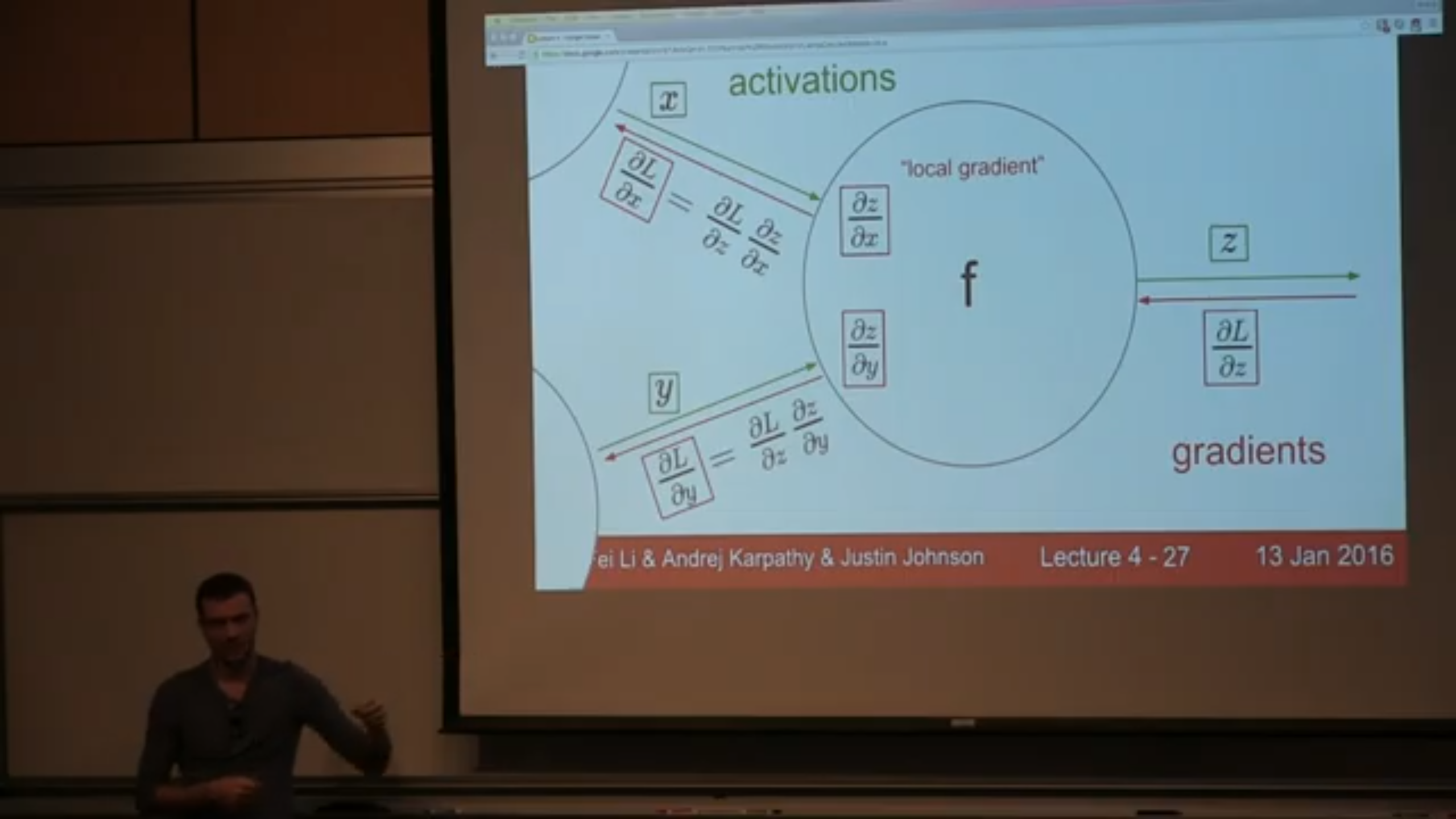
图3来自CS231n课程的视频截图（卡帕西老师讲的课），在每个节点（激活函数）都可以计算节点输 出（$z$）对输入（$x$, $y$）的“本地”偏导数（“local gradient”），因为在当前节点，只要知道 了输入和输出是什么，就可以计算出“本地”偏导数。那么，如图中所示，在反向传播过程中，（例如） 倒数第一个节点就是计算损失函数$L$对节点输出$z$的偏导数$\frac{\partial L}{\partial z}$， 那怎么计算输入对损失函数的影响程度呢？链式法则。利用已经计算好存起来的本地梯度值 （$\frac{\partial z}{\partial x}$），通过链式法则可以快速计算得到节点输入$x$或$y$对损 失函数$L$的偏导数（如图所示）。这个过程是递归式的。

反向传播的目的就是计算梯度，而计算梯度就是为了更新权重。

(注: 1.针对单隐藏层的反向传播过程的每一步的计算公式细节，请《动手学深度学习》第4章。 2.如果对理论层面的内容感兴趣可以看看我的另一个博客，或直接参考“西瓜书³”的相关章节)

## 静态计算图 vs 动态计算图

在执行前向传播和反向传播时，计算图会帮助管理和追踪各个操作，确保梯度能够顺利传播到每一个 参数。PyTorch 的计算图之所以被称为 “动态生成的”，是因为它 在每次前向传播时都会重新构建一 次计算图，而不是像一些静态计算图框架（如 TensorFlow 1.x）那样在训练开始前定义好固定的计 算图。

在静态计算图（如 TensorFlow 1.x）中，模型在训练开始前需要构建完整的计算图，整个计算图在 训练过程中是固定的。优点是执行效率高，因为优化器可以对整个图进行优化。缺点是灵活性差，若 需要调整模型结构（比如根据条件使用不同的层），则需要重新构建计算图。

PyTorch 使用的动态计算图（也称为“define-by-run”），在每次前向传播时都会重新构建计算图。 优点是灵活性高，适合处理结构复杂或变化的网络，例如循环神经网络或条件分支模型。因为每次执 行前向传播时可以定义不同的操作，使得网络结构可以基于运行时的输入或状态动态调整。缺点是计 算图的构建可能稍微增加了开销，但这对大部分模型来说影响很小。

Pytorch的计算图由节点和边组成，节点表示张量或者Function，边表示张量和Function之间的依赖 关系。

Pytorch的动态计算图的“动态”主要有两重含义：

• 第一层含义是：计算图的正向传播是立即执行的。无需等待完整的计算图创建完毕，每条语句都会 在计算图中动态添加节点和边，并立即执行正向传播得到计算结果。

• 第二层含义是：计算图在反向传播后立即销毁。下次调用需要重新构建计算图。如果在程序中使用 了backward方法执行了反向传播，或者利用torch.autograd.grad方法计算了梯度，那么创建 的计算图会被立即销毁，释放存储空间，下次调用需要重新创建。

#计算图在反向传播后立即销毁，
#loss.backward(retain_graph = True) # 如果需要保留计算图, 需要设置retain_graph = True
loss.backward()
#loss.backward()                    # 否则如果再次执行反向传播将报错

## Funciton 节点

除了张量节点，计算图中的另外一种节点是Function, 实际上就是 Pytorch中各种对张量操作的函数。

这些Function和我们Python中的函数有一个较大的区别，那就是它同时包括正向计算逻辑和反向传播 的逻辑。

我们可以通过继承torch.autograd.Function来创建这种支持反向传播的Function：

class MyReLU(torch.autograd.Function):

    #正向传播逻辑，可以用ctx存储一些值，供反向传播使用。
    @staticmethod
    def forward(ctx, input):
        ctx.save_for_backward(input)
        return input.clamp(min=0)

    #反向传播逻辑
    @staticmethod
    def backward(ctx, grad_output):
        input, = ctx.saved_tensors
        grad_input = grad_output.clone()
        grad_input[input < 0] = 0
        return grad_input


relu = MyReLU.apply # relu现在也可以具有正向传播和反向传播功能
Y_hat = relu(X@w.t() + b)
loss = torch.mean(torch.pow(Y_hat-Y,2))

loss.backward()

print(Y_hat.grad_fn) # Y_hat的梯度函数即是我们自己所定义的 MyReLU.backward

## 计算图与反向传播

loss.backward()语句调用后，依次发生以下计算过程。

1. loss自己的grad梯度赋值为1，即对自身的梯度为1。

2. loss根据其自身梯度以及关联的backward方法，计算出其对应的自变量即y1和y2的梯度，将该值 赋值到y1.grad和y2.grad。

3. y2和y1根据其自身梯度以及关联的backward方法, 分别计算出其对应的自变量x的梯度， x.grad将其收到的多个梯度值累加。

注意，1,2,3步骤的求梯度顺序和对多个梯度值的累加规则恰好是求导链式法则的程序表述。

正因为链式求导法则衍生的梯度累加规则，张量的grad梯度不会自动清零，在需要的时候需要手动置零。

import torch

x = torch.tensor(3.0,requires_grad=True)
y1 = x + 1
y2 = 2*x
loss = (y1-y2)**2

loss.backward()

print("loss.grad:", loss.grad)
print("y1.grad:", y1.grad)
print("y2.grad:", y2.grad)
print(x.grad)

## 叶子节点和非叶子节点

loss.backward()

print("loss.grad:", loss.grad)          # None，预期是tensor(1.0)
print("y1.grad:", y1.grad)              # None，预期是tensor(-4.0)
print("y2.grad:", y2.grad)              # None，预期是tensor(4.0)
print(x.grad)                           # tensor(4.0)

执行上面代码，我们会发现loss.grad并不是我们期望的1,而是 None。

类似地y1.grad以及y2.grad也是 None.

这是为什么呢？这是由于它们不是叶子节点张量。

反向传播过程中，只有is_leaf=True的叶子节点，需要求导的张量的导数结果才会被最后保留下来。

那么什么是叶子节点张量呢？叶子节点张量需要满足两个条件。

• 叶子节点张量是由用户直接创建的张量，而非由某个Function通过计算得到的张量。
• 叶子节点张量的requires_grad属性必须为True.

Pytorch设计这样的规则主要是为了节约内存或者显存空间，因为几乎所有的时候，用户只会关心他 自己直接创建的张量的梯度。

所有依赖于叶子节点张量的张量, 其requires_grad属性必定是True的，但其梯度值只在计算过程 中被用到，不会最终存储到grad属性中。

如果需要保留中间计算结果的梯度到grad属性中，可以使用retain_grad方法。 如果仅仅是为了调试代码查看梯度值，可以利用register_hook打印日志。

#非叶子节点梯度显示控制
y1.register_hook(lambda grad: print('y1 grad: ', grad))
y2.register_hook(lambda grad: print('y2 grad: ', grad))
loss.retain_grad()
#反向传播
loss.backward()

以上代码片段均来自“eat_pytorch_in_20_days”，更多PyTorch细节，可以参考https://github.com/lyhue1991/eat_pytorch_in_20_days/

另一个也比较详细讲解动态图求偏导数过程的博客是这个https://yey.world/2020/12/08/Pytorch-04/

# 整个故事框架：梯度下降算法和反向传播算法

神经网络的权重更新是通过梯度下降或其变体算法实现的。梯度下降的核心思想是通过反向传播 计算出损失函数对每个权重的梯度，然后利用这些梯度信息调整权重，使损失逐步减小（最优化过 程），从而提高模型的预测能力。以下是权重更新的详细步骤：

## 1. 计算损失函数

在前向传播完成后，神经网络会计算损失函数 $L$，它衡量模型预测值与真实值之间的差异。例 如，常用的损失函数包括均方误差（用于回归任务）和交叉熵损失（用于分类任务）。

## 2. 反向传播：计算损失对权重的梯度

在反向传播过程中，通过链式法则计算损失对每层权重的梯度。对于每个权重矩阵 $W$ ，我们会得 到一个梯度矩阵 $\frac{\partial L}{\partial W}$，这个矩阵表示损失函数 $L$ 对 $W$ 的敏感度。

## 3. 梯度下降更新权重

使用梯度下降算法更新权重。对于每个权重 $W$，更新规则为：

$$ W = W - \eta \cdot \frac{\partial L}{\partial W} $$

其中：

• $\eta$ 是学习率，决定了每次更新的步长大小。
• $\frac{\partial L}{\partial W}$ 是损失对权重的梯度。

## 4. 不同的优化算法

经典的梯度下降可以分为以下几种方式：

• 批量梯度下降（Batch Gradient Descent）：在整个训练数据集上计算梯度并更新权重。这种 方法计算较慢但更新稳定。
• 随机梯度下降（Stochastic Gradient Descent, SGD）：对每个样本计算一次梯度并更新权重， 计算速度快，但会引入噪声，使得更新方向不稳定。
• 小批量梯度下降（Mini-Batch Gradient Descent）：在一个小批量上计算梯度和更新权重， 兼顾了效率和稳定性。

此外，还有一些常见的梯度优化算法的变体，用来提高收敛速度和稳定性：

• 动量法（Momentum）：在更新时加入上一次的梯度，缓解方向震荡并加速收敛。

• Adam（Adaptive Moment Estimation）：结合动量法和RMSProp，根据过去的梯度平均值和均 方根值调整学习率，使得每个权重的更新幅度自适应。

• RMSProp：通过历史梯度的平方和来调整学习率，防止震荡，特别适合处理稀疏梯度。

## 5. 迭代更新

在整个训练过程中，通过不断进行前向传播、反向传播和梯度更新，模型的权重逐渐优化，从而使损 失函数逐步减小。这个迭代过程会持续进行，直到满足训练结束的条件（如达到设定的轮次或损失足 够小）。