fgg blog

变分自编码器（VAE）

/posts/neuralnetworks/variationalautoencoder/ map[email:1522009317@qq.com name:fmh]
Table of Contents

## 变分自编码器：Veriational AutoEncoder (VAE)

# 自编码器

自编码器通常用于数据压缩，也就是将高维数据映射到低维空间，然后通过解码器对压缩后的数据进 行重构（尝试恢复原数据）。例如：在训练阶段，将214x214的图片通过解码器压缩为100维的向量， 然后用解码器对这个100维向量进行重构，重构的目标是生成的图片与原图片越接近越好。经过大量 数据训练后，模型将学会对数据进行压缩。

图像去噪(de-noicing)：如果在训练过程，给输入数据加入噪音信号，重构目标是原图片，则模型同 时学会降噪；

图像分割(segmentation)：如果在训练过程，输入数据不变，而重构目标变成图像区块，则模型学会 分割；

神经填充(neural inpainting)：如果在训练过程，直接对图片部分内容打码，而重构目标是原图片， 则模型学会还原被打码部分(最近闹得沸沸扬扬的“一键消衣，无中生胸”大约是此类模型技术)；

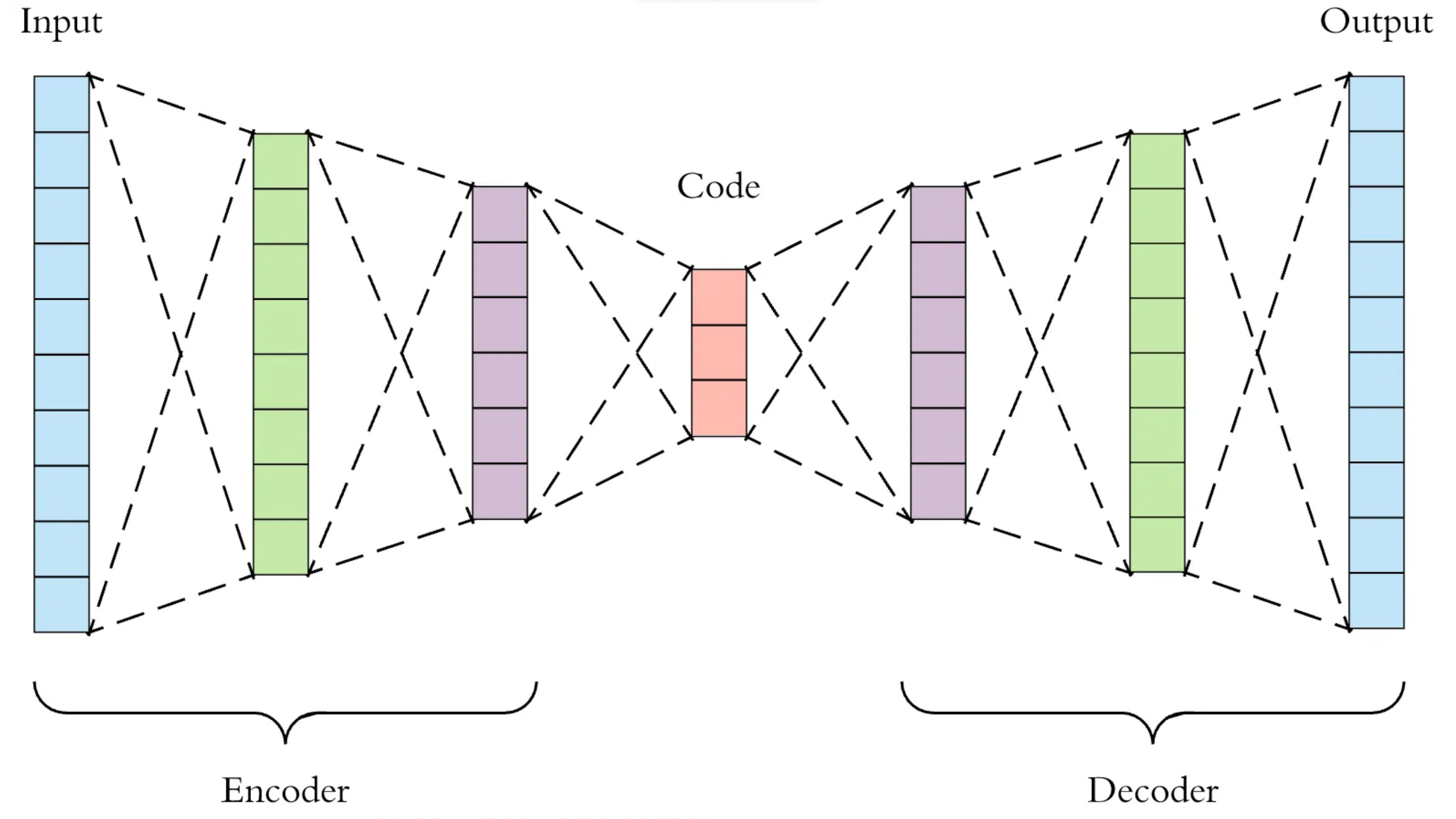
IMG_AE

# 变分自编码器

变分自编码器（VAE）是一种生成模型，结合了自编码器和概率图模型的思想。

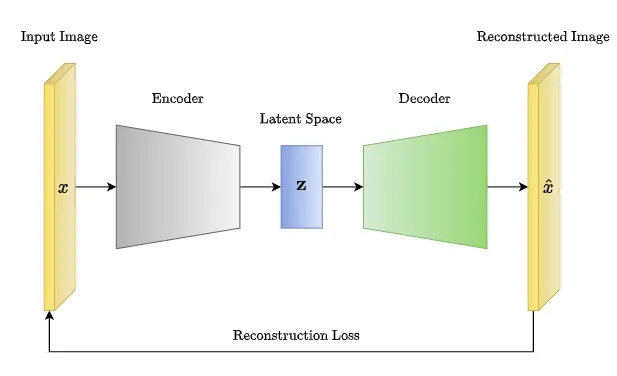
变分自编码器中的模型架构与自编码器一样，区别主要在于生成的低维表示的方式，自编码器 是生成固定长度的向量，然后传递给解码器；但变分自编码器则生成一个潜在空间中的概率分布 （laten space distribution），然后从这个分布采样得到的数据再传递给解码器。

变分自编码器中的“变分”其实是“概率推断”（probabilistic inference）中的一种技术，称为“变分 推断（variational inference）。在概率图模型中，通常需要计算后验概率分布（posterior dist.）， 即贝叶斯分析中的后验概率。而对于复杂的概率模型，这个后验概率难以直接计算。 解决这个后验概率计算的思路有两种：一是MCMC方法；二就是变分推断。两者都是近似计算方法。

  • MCMC（马尔科夫链蒙特卡洛）是通过构建满足平稳分布为目标分布的马尔科夫链，然后待马尔科夫 链收敛到平稳分布后，就从这个分布抽样。

  • VI（变分推断）就是通过优化一个参数化的近似分布来近似真实的后验分布，试图将推断问题转变 成最优化问题。更多关于VI的内容请移步这里。

VAE的工作流程如下：

  1. 编码器（Encoder）：将输入数据映射到潜在空间中的分布参数。这个过程可以理解为将输入数据 编码成潜在空间中的概率分布，而不是直接映射到一个确定的点。

  2. 采样（Sampling）：从潜在空间的分布中采样一个点，作为潜在表示（latent representation）。

  3. 解码器（Decoder）：将潜在表示解码为输出数据的概率分布。与编码器相对应，解码器将潜在表 示映射回原始数据的分布参数。

  4. 重构损失（Reconstruction Loss）：衡量重构数据与原始数据之间的差异，通常使用重构误差或 者交叉熵来衡量。

  5. KL 散度损失（KL Divergence Loss）：用于度量编码器输出的潜在分布与预设的先验分布（通常 是高斯分布）之间的差异，促使模型学习到合理的潜在表示。

  6. 总损失（Total Loss）：重构损失和KL散度损失的加权和，用于训练模型。

IMG_AE

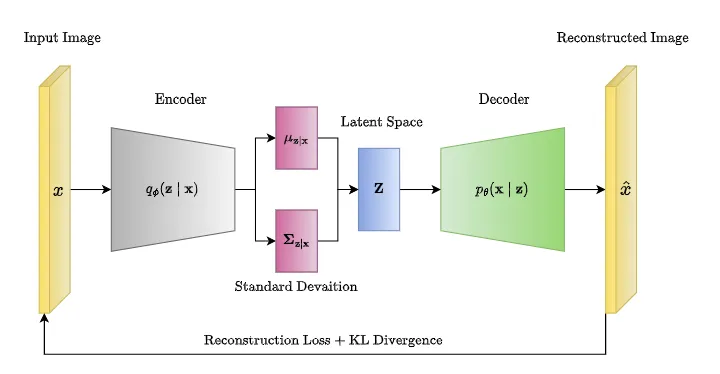
IMG_VAE

# 重参数化技巧（reparametrization trick）

在标准的VAE中，编码器网络通常会输出潜在空间中的均值（mean）和标准差（standard deviation），然后通过从该分布中采样来生成潜在表示。然而，直接从均值和标准差中采样是不可 微的，这导致了无法直接使用梯度下降来训练模型。

Reparametrization Trick 的关键思想是重新参数化潜在表示的采样过程，使得采样操作与网络参数 之间的关系变得可导。具体而言，潜在表示 $\mathbf{z}$ 通过一个确定的变换从一个固定的标准高 斯分布中采样得到，然后通过编码器网络的输出来计算这个变换的参数。这个过程可以表示为：

$$ z = \mu + \sigma \odot \epsilon $$

其中，$\mu$ 是编码器网络输出的均值，$\sigma$ 是输出的标准差，$\epsilon$ 是从标准正态分布 $N(0, 1)$ 中采样得到的噪声。

通过这种重新参数化，$\mathbf{z}$ 的采样过程与模型参数的梯度相关，从而使得可以直接使用梯 度下降算法来优化模型参数。这种技巧允许我们在训练过程中，通过反向传播算法直接更新编码器和 解码器的参数，从而优化VAE模型。

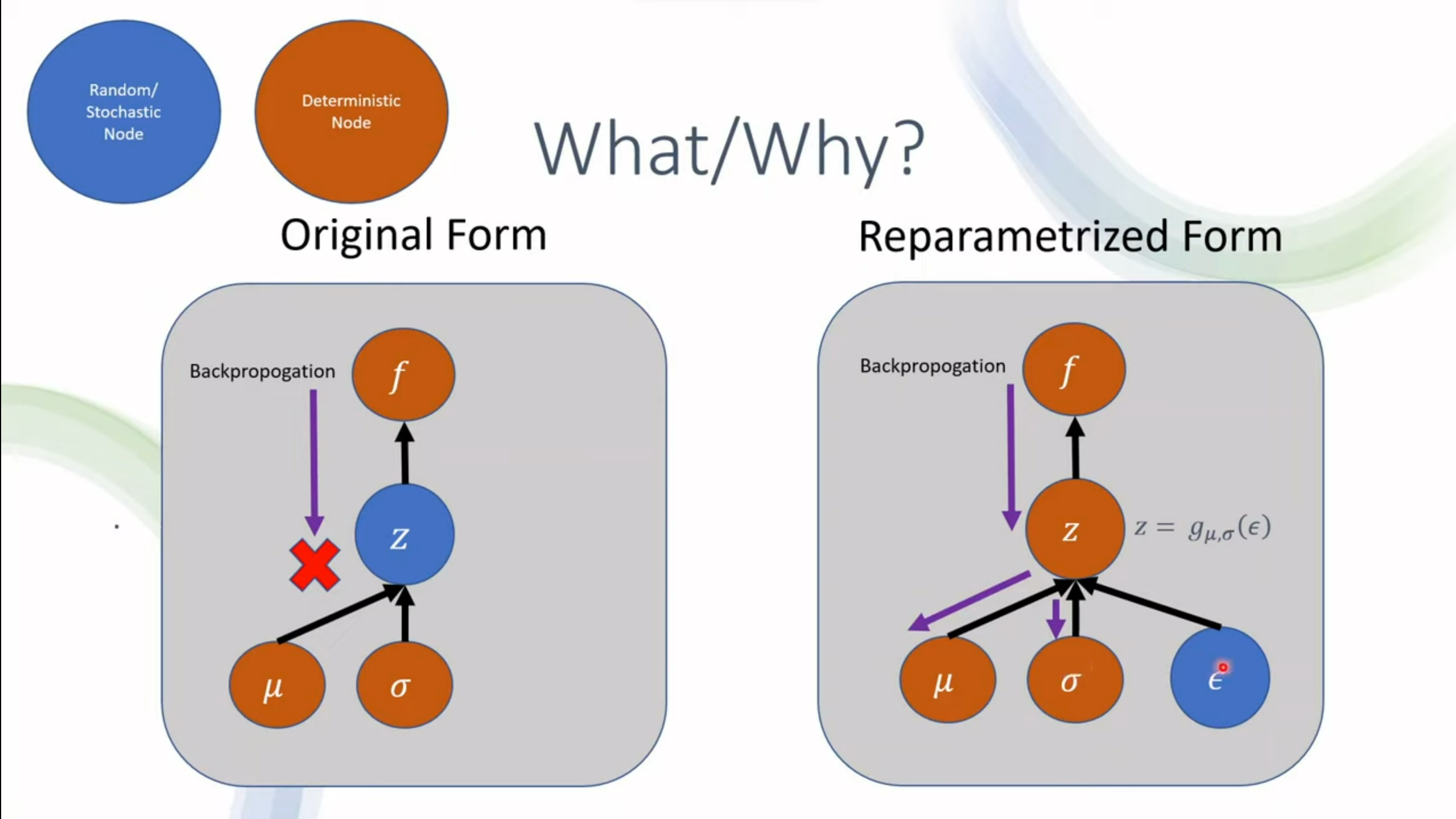
IMG_VAE_trick

# $\beta$-VAE (Disentangled VAE)

在损失函数中，使用一个超参数 $\beta$ 乘以 KL-散度损失。也就是：

$$ Loss = \text{Reconstruction Loss} + \beta \times \text{KL Divergence} $$

其中，β 是一个超参数，用于平衡重构损失和 KL 散度之间的重要性。通过调整 β 的值，可以控制 模型对潜在表示的约束程度。当 β=1 时，与标准的VAE相等，而当 β 小于1 时，模型更加关注于重 构损失，从而更加注重数据的重建；当 β 大于1 时，模型更加关注于 KL 散度，从而更加注重潜在 表示的独立性和结构性。