# 变分推理¹

变分推理是贝叶斯学习中常用的、含有隐变量模型的学习和推理方法。变分推理和MCMC²属于不同 的技巧。MCMC通过随机抽样的方法近似地计算模型的后验概率，变分推断则通过解析的方法计算模型 的后验概率的近似值。

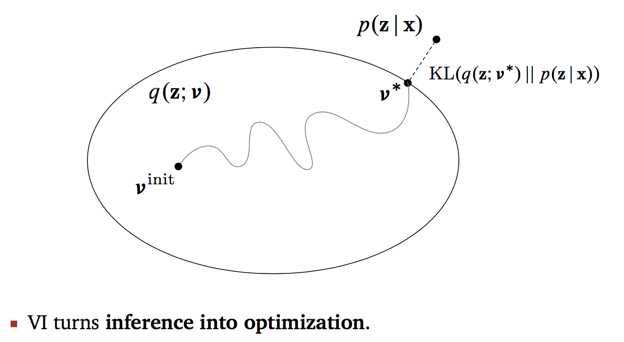
变分推理基本思想： 假设模型是联合概率分布 $p(x,z)$ ，其中 $x$ 是观测变量（i.e., 数据），$z$ 是隐变量，包括 参数。目标是学习模型的后验概率分布 $p(z|x)$ 和用模型进行概率推理。但这是一个复杂的分布， 直接估计分布的参数很困难。所以考虑用概率分布 $q(z)$ 近似条件概率分布 $p(z|x)$ ，用KL散度 $D(q(z)||p(z|x))$ 计算两者的相似度，$q(z)$ 被称为“变分分布（variational distribution）”。 如果能找到与 $p(z|x)$ 在KL散度意义下最近的分布 $q^{*}(z)$ ，则可以用这个分布近似$p(z|x)$。

$$ p(z|x) \approx q^{*}(z) $$

## 关于 KL散度和证据下界

KL散度³可以写成以下形式

$$ \begin{eqnarray} D(q(z)||p(z|x)) &=& E_{q} [\log q(z)] - E_{q} [\log p(z|x)] \\ &=& E_{q} [\log q(z)] - E_{q} [\log p(z,x)] + \log p(x) \\ &=& \log p(x) - \{ E_{q} [\log p(z,x)] - E_{q} [\log q(z)] \} \end{eqnarray} $$

由KL散度性质可知上式中：

$$ \begin{eqnarray} \log p(x) \ge E_{q} [\log p(z,x)] - E_{q} [\log q(z)] \end{eqnarray} $$

不等式右端是左端的下界，左端称为“证据（evidence）”，右端称为“证据下界（evidence lower bound, ELBO）”，证据下界记作：

$$ \begin{eqnarray} L(q) = E_{q} [\log p(z,x)] - E_{q} [\log q(z)] \end{eqnarray} $$

KL散度的最小化可以通过证据下界的最大化实现，因为目标是求 $q(z)$ 使KL散度最小化。因此，变分推理变成求解证据下界最大化问题。 通过迭代的方法最大化证据下界，这时可以使用“变分EM算法”。

## 关于 $q(z)$

对变分分布 $q(z)$ 的要求是具有容易处理的形式，通常假设 $q(z)$ 对 $z$ 的所有分量都是互相 独立的（实际是条件独立于参数），即满足

$$ q(z) = q(z_1) q(z_2) \cdots q(z_n) $$

此时的变分分布也叫作“平均场（mean field）”。KL散度的最小化或证据下界最大化实际是在平均场 的集合，即满足独立假设的分布集合 $Q = {q(z)|q(z)=\prod^{n}_{i=1}q(z_i)}$ 之中进行的。