变分推理是贝叶斯学习中常用的、含有隐变量模型的学习和推理方法。变分推理和MCMC2属于不同 的技巧。MCMC通过随机抽样的方法近似地计算模型的后验概率,变分推断则通过解析的方法计算模型 的后验概率的近似值。
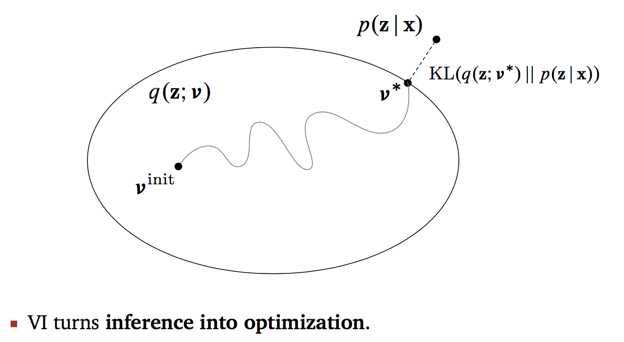
变分推理基本思想: 假设模型是联合概率分布 $p(x,z)$ ,其中 $x$ 是观测变量(i.e., 数据),$z$ 是隐变量,包括 参数。目标是学习模型的后验概率分布 $p(z|x)$ 和用模型进行概率推理。但这是一个复杂的分布, 直接估计分布的参数很困难。所以考虑用概率分布 $q(z)$ 近似条件概率分布 $p(z|x)$ ,用KL散度 $D(q(z)||p(z|x))$ 计算两者的相似度,$q(z)$ 被称为“变分分布(variational distribution)”。 如果能找到与 $p(z|x)$ 在KL散度意义下最近的分布 $q^{*}(z)$ ,则可以用这个分布近似$p(z|x)$。
$$ p(z|x) \approx q^{*}(z) $$